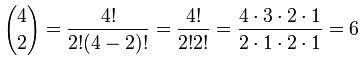Dear Children,
Prepare to be surprised to discover how versatile Pascal's triangle is. Amazing and amusing at the same time - exploring Pascal's Triangle will lead you down an unforgettable path. Don't forget to tell your Math teacher about what you learnt from this.
The information here has been sourced from http://www.mathsisfun.com/pascals-triangle.html .
Prepare to be surprised to discover how versatile Pascal's triangle is. Amazing and amusing at the same time - exploring Pascal's Triangle will lead you down an unforgettable path. Don't forget to tell your Math teacher about what you learnt from this.
The information here has been sourced from http://www.mathsisfun.com/pascals-triangle.html .
Pascal's Triangle
One of the most interesting Number Patterns is Pascal's Triangle (named after Blaise Pascal, a famous French Mathematician and Philosopher).
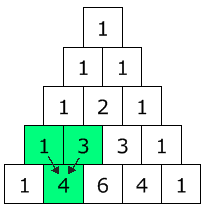
To build the triangle, start with "1" at the top, then continue placing numbers below it in a triangular pattern.
Each number is the numbers directly above it added together.
(Here I have highlighted that 1+3 = 4)
|  |
Patterns Within the Triangle
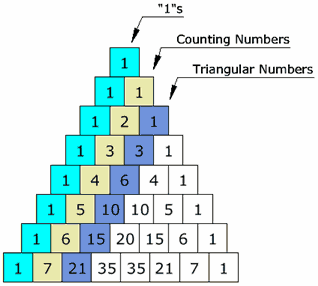 | Diagonals
The first diagonal is, of course, just "1"s, and the next diagonal has the Counting Numbers (1,2,3, etc).
The third diagonal has the triangular numbers
(The fourth diagonal, not highlighted, has thetetrahedral numbers.)
|
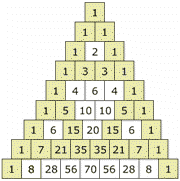
Odds and Evens
If you color the Odd and Even numbers, you end up with a pattern the same as the Sierpinski Triangle
|  |
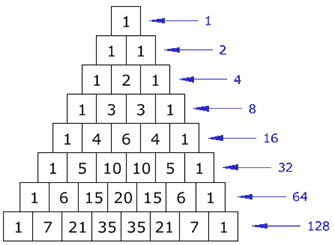 | Horizontal Sums
What do you notice about the horizontal sums?
Is there a pattern? Isn't it amazing! It doubles each time (powers of 2).
|
Exponents of 11
Each line is also the powers (exponents) of 11:
| 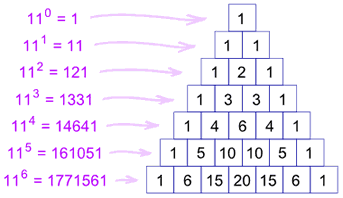 | |
But what happens with 115 ? Simple! The digits just overlap, like this: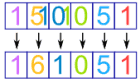
The same thing happens with 116 etc.
| ||
Squares
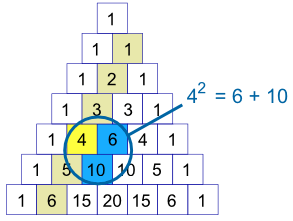
For the second diagonal, the square of a number is equal to the sum of the numbers next to it and below both of those.
Examples:
There is a good reason, too ... can you think of it?
(Hint: 42=6+10, 6=3+2+1, and 10=4+3+2+1) |
Fibonacci Sequence
Try this: make a pattern by going up and then along, then add up the values (as illustrated) ... you will get the Fibonacci Sequence.
(The Fibonacci Sequence starts "0, 1" and then continues by adding the two previous numbers, for example 3+5=8, then 5+8=13, etc) | 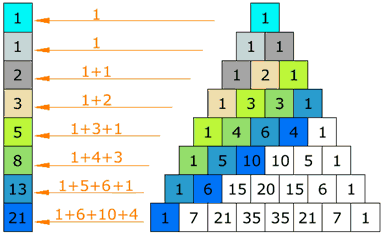 |
 | Symmetrical
And the triangle is also symmetrical. The numbers on the left side have identical matching numbers on the right side, like a mirror image.
|
Using Pascal's Triangle
Heads and Tails
Pascal's Triangle can show you how many ways heads and tails can combine. This can then show you the probability of any combination.
For example, if you toss a coin three times, there is only one combination that will give you three heads (HHH), but there are three that will give two heads and one tail (HHT, HTH, THH), also three that give one head and two tails (HTT, THT, TTH) and one for all Tails (TTT). This is the pattern "1,3,3,1" in Pascal's Triangle.
| Tosses | Possible Results (Grouped) | Pascal's Triangle |
|---|---|---|
| 1 | H T | 1, 1 |
| 2 | HH HT TH TT | 1, 2, 1 |
| 3 | HHH HHT, HTH, THH HTT, THT, TTH TTT | 1, 3, 3, 1 |
| 4 | HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT | 1, 4, 6, 4, 1 |
| ... etc ... |
Combinations
The triangle also shows you how many Combinations of objects are possible.
A Formula for Any Entry in The Triangle
In fact there is a formula from Combinations for working out the value at any place in Pascal's triangle:
It is commonly called "n choose k" and written like this:
| 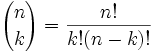 |
Notation: "n choose k" can also be written C(n,k), nCk or even nCk.
 |
The "!" is "factorial" and means to multiply a series of descending natural numbers. Examples:
|
So Pascal's Triangle could also be
an "n choose k" triangle like this:
(Note how the top row is row zero
and also the leftmost column is zero) | 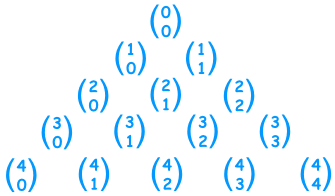 |
This can be very useful ... you can now work out any value in Pascal's Triangle directly (without calculating the whole triangle above it).
Polynomials
Pascal's Triangle can also show you the coefficients in binomial expansion:
| Power | Binomial Expansion | Pascal's Triangle |
|---|---|---|
| 2 | (x + 1)2 = 1x2 + 2x + 1 | 1, 2, 1 |
| 3 | (x + 1)3 = 1x3 + 3x2 + 3x + 1 | 1, 3, 3, 1 |
| 4 | (x + 1)4 = 1x4 + 4x3 + 6x2 + 4x + 1 | 1, 4, 6, 4, 1 |
| ... etc ... |
The First 15 Lines
For reference, I have included row 0 to 14 of Pascal's Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
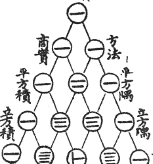 | The Chinese Knew About It
This drawing is entitled "The Old Method Chart of the Seven Multiplying Squares". View Full Image
It is from the front of Chu Shi-Chieh's book "Ssu Yuan Yü Chien" (Precious Mirror of the Four Elements), written in AD 1303 (over 700 years ago, and more than 300 years before Pascal!), and in the book it says the triangle was known about more than two centuries before that.
|
The Quincunx
 | An amazing little machine created by Sir Francis Galton is a Pascal's Triangle made out of pegs. It is called The Quincunx. Balls are dropped onto the first peg and then bounce down to the bottom of the triangle where they collect in little bins.
|
Regards,
Tanvi Ma'am